Patrones matemáticos y arte

Desde hace muchos años, el arte suele frecuentar los mismos caminos que la matemática. De la misma forma que lo hacen otras disciplinas. Para comprender un poco de esta relación, se hace necesario remitirnos a los antiguos griegos, en donde intrínsecamente todas las áreas del conocimiento se encontraban conectadas. En aquella época utilizaron a la matemática para describir patrones en la naturaleza en un intento por descubrir un patrón que lo rigiera todo en el mundo. Y ciertamente dieron con varios.

El número representado por la letra griega φ (phi) es uno de los patrones más conocidos. Que quede claro que Phi y Pi son números racionales, pero completamente distintos. El número áureo (o Phi) equivale a aproximadamente 1.618 (dado que es una magnitud irracional el uso del número redondeado es algo común). El número Phi está directamente relacionado con la Secuencia de Fibonacci. Ambos componen lo que se conoce como proporción aurea que puede encontrarse en cosas tan grandes como el movimiento del universo y tan pequeñas como la distribución atómica. El número Phi es omnipresente en la arquitectura, tanto en edificaciones del pasado como del presente. El número Phi está presente en la música, en las obras de Beethoven. El número Phi está en el cine, entre las obras de muchos editores pero especialmente entre las del ruso Sergei Eisenstein, que en su película “El acorazado Potemkin” midió las estructuras y los tiempos para que coincidieran con el número Phi.

Un video de 1959 que nos cuenta un poco sobre los patrones en la naturaleza.

El número Phi se encuentra entre la naturaleza, en los patrones de crecimiento de las semillas de girasol, en los pétalos del jazmín y en el crecimiento de la concha del Nautilus pompilius. En las medidas de varias distancias del cuerpo humano, por ejemplo, mide desde la punta de tu dedo medio hasta el hombro y desde la punta del dedo medio hasta el codo, divide… ahí esta Phi. En la sonrisa de esa persona que tanto te gusta, la medida de los dientes encaja en la Secuencia de Fibonacci. El ojo humano es fácil de dibujar repitiendo la espiral de Fibonacci múltiples veces.

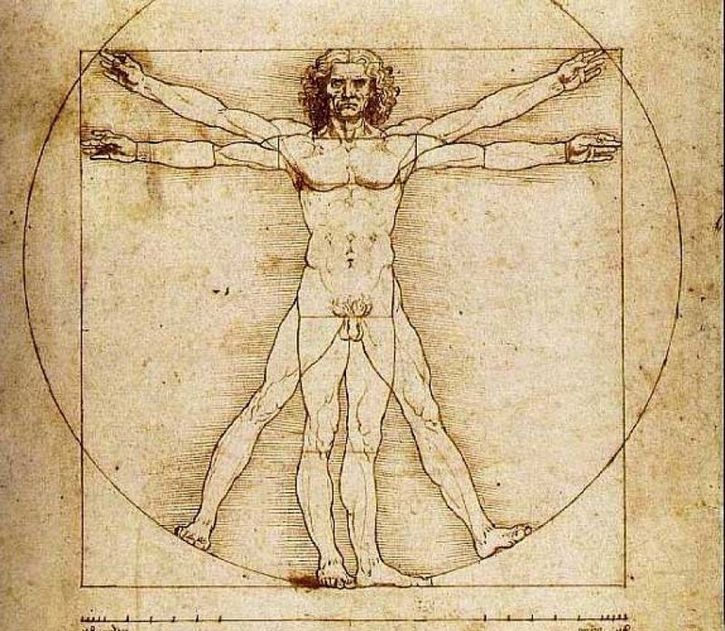
En el mundo del arte la mayor representación de Phi la hizo Da Vinci, que en todas sus obras se preocupó de encajar de alguna forma Phi, ya fuera en las medidas del rostro de la Mona Lisa o en la distancia entre Jesús y sus discípulos en la Última cena. Más importante que eso, el Hombre de Vitruvio representa las medidas perfectas y reales. En su cuerpo se ocultan varias operaciones matemáticas que si se resuelven resultan en Phi. Y no es la única armonía que encontramos en estos parajes de los patrones matemáticos.

Actualmente se estudia otro tipo de patrón conocido como Fractal, los fractales son considerados figuras geométricas no euclidianas provistas de auto semejanza, recursividad, holismo y amplificación. Pero vayamos por partes que así se hace difícil comprender la idea. Una figura no euclidiana es aquella que no encaja en la geometría que nos enseñan en la escuela. Diferente a las demás figuras, esta es generada por un “caos organizado” que produce patrones de cierta belleza y (créelo) sin valores exactos, también frutos de la irracionalidad.

¿Y dónde encontramos esos fractales? Viendo a una montaña, a una cuenca, en el crecimiento de las plantas, en la formación de cristales en el hielo. ¿Y para qué nos sirve estudiar estos fractales? La formación cristalina se basa en fractales, y dependiendo de la formación, podemos fabricar no solamente materiales más resistentes sino también medicamentes más eficientes. Los fractales también son recurridos en las artes plásticas y hasta en la programación de computadoras.

Cuando decimos que los fractales tienen auto-semejanza, esto significa que cualquier parte pequeña de todo el conjunto será igual a todas las otras representadas. Por ejemplo, cuando un árbol crece y las ramas salen de sus capullos (pequeños embriones distribuidos por el tronco) son iguales a todas las demás producidas por el árbol. Ahí reside la recursividad, la repetición del patrón. Holismo significa amplificación, en palabras más simples sería decir que la tendencia de estas figuras es siempre crecer y crecer sin llegar a un resultado determinado.

Por último, pero no menos importante, el patrón toro nos habla de un anillo parecido a una dona, la cual se mantiene en movimiento, provocando que la parte exterior vaya al centro del anillo por arriba, saliendo por abajo. El patrón toro puede aplicarse en la producción de energía autosustentable. La empresa Pax Scientific patentó un modelo de producción de energía basado en un toro. En el arte marcial Aikido el patrón toro también se observa, cuando una de las lecciones más importantes trata de seguir el flujo de energías del universo.

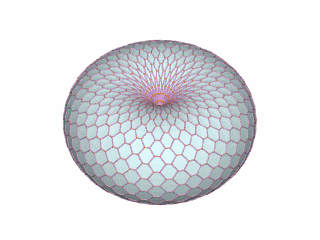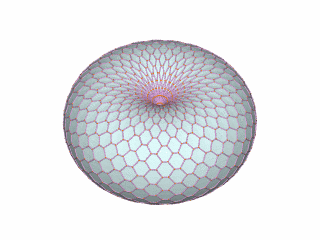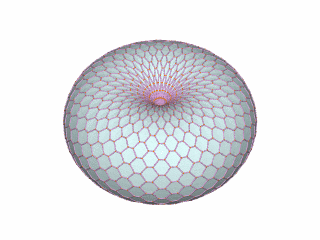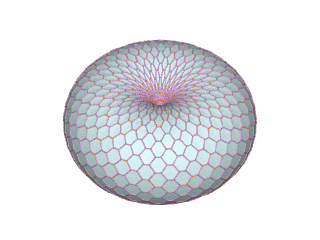
Abriendo un poco la mente, el filósofo Ashok Gangadean señala que todos nosotros compartimos una vida llena de experiencias distintas y unificadas. Así como el toro es una figura distinta y unificada, todos nosotros somos seres distintos y unificados en una humanidad. El filósofo muestra que al combinar nuestras experiencias y unificar nuestros cuerpos distintos compartiendo la experiencia a través del diálogo, damos lugar a un patrón toro. Y no es una tendencia exclusiva del individuo, sino también de las sociedades. Si viviéramos solos con nuestras experiencias no ampliaríamos el conocimiento, pero si unificamos nuestras experiencias a través del dialogo, incrementamos nuestro campo de pensamiento y creatividad. En sí, nuestra propia conciencia actúa en un patrón de toro.

Tanto en la vida más externa como en el campo más personal y metafísico, los patrones matemáticos, incluso si no representan un resultado racional, rigen nuestros movimientos. Pero eso no significa que no tengamos libre albedrio, pues por encima de todo son nuestros movimientos los que definen dichos patrones, y no los patrones los que definen nuestros movimientos.