El infinito no es un número, no es una medida: es una abstracción que representa lo que no tiene límite o fin. El conjunto de los números naturales, por ejemplo, es infinito, porque no importa qué número se tenga, siempre se le puede agregar 1 para obtener el número siguiente.

A pesar de que la representación de una idea, no es un número, el infinito tiene algunas propiedades numéricas que nos permiten trabajar con él. Por ejemplo, si representamos esta idea con el símbolo ∞, se puede escribir 1 + ∞ = ∞, lo cual puede ser interpretado como «si hay algo que no tiene fin, se puede agregar uno y todavía seguirá sin fin.»
Lo más importante acerca de la infinidad es que – ∞ < x < ∞, donde x es un número real, que es una abreviación para la frase «menos infinito es menor que cualquier número real, e infinito es mayor que cualquier número real»
Algunas operaciones con ∞ son indefinidas, por ejemplo, ∞ + ∞ = ∞, o – ∞ + – ∞ = ∞. Además, también hay conjuntos con infinitos elementos, y la idea de tamaños diferentes sin fin. Pero lo más extraño son las paradojas que tenemos con números infinitos. Una paradoja es una noción verdadera que desafía nuestra intuición, o incluso la lógica. Estas son algunas de las paradojas que implican al infinito:
1. Hotel de Hilbert.

Imagínese un hotel de infinitas habitaciones en el que todas están ocupadas. Un viajero llega al hotel y solicita hospedaje. Sólo que no tienen espacios, a pesar del sinfín de habitaciones, el hotel ya está totalmente ocupado.
Pero el gerente es un tipo que no deja a nadie sin habitación, y hace lo siguiente: pide que el huésped del cuarto 1 se pase a la habitación 2, el huésped de la habitación 2 pase a la habitación 3, el huésped de la habitación 3 haga el movimiento a la 4 y así sucesivamente.
Y voila, el hotel que estaba lleno, ahora tiene una vacante para el nuevo huésped. Con esta estrategia, el gerente del hotel tiene capacidad para un nuevo huésped, 10 nuevos huéspedes, un millón de nuevos huéspedes, o incluso un número infinito de nuevos huéspedes.
Esta paradoja fue propuesta por el matemático alemán David Hilbert, y es una paradoja, porque nuestra definición de hotel lleno es que no hay vacantes para los nuevos clientes. Pero si tenemos infinitas habitaciones, aunque todos ellas están llenas, tienen para dar cabida a una serie de nuevos huéspedes, incluso infinitos.
2. Trompeta de Gabriel

La trompeta de Gabriel, la trompeta del ángel Gabriel, o la trompeta de Torricelli es una superficie en forma de embudo (o de trompeta). Empieza ancha y se estrecha rápidamente, pero nunca se cierra – es decir, sigue hasta el infinito.
La superficie de la trompeta es infinita, pero el volumen que la envuelve no es infinito (una idea matemática). Supongamos que usted tiene que pintar la trompeta de color oro del lado interior de esta. La superficie de la misma es infinita, entonces necesita una cantidad infinita de pintura, ¿verdad? Bueno, puedes tomar una cantidad finita de pintura, que corresponde al volumen de la trompeta, y aplicar esta pintura en la trompeta, dejando que se escurra.
A continuación, puedes elegir entre lo que te dejara más confundido: si una superficie infinita implica un volumen finito, o si una cantidad finita de pintura cubre una superficie infinita.
El discípulo de Galileo, Torricelli, fue el primero en pensar en este problema, que encontró tan extraordinario que en un principio pensó que había hecho algo malo. Otros filósofos y matemáticos estaban tan horrorizados con las paradojas que surgieron con el infinito, que llegaron a proponer la idea del destierro.
3. El enigma del juego de los dardos.

Suponga que tiene un blanco, un dardo, y la certeza del 100% de que acertarás al blanco en alguna parte. Ahora piensa en la punta del dardo, el punto matemático exacto de extremidad, y piensa en el punto matemático del blanco. La pregunta es, ¿cuál es la probabilidad de que ese punto sea alcanzado por el dardo?
Podemos comenzar suponiendo que hay una posibilidad mayor que cero de que el punto sea golpeado por la punta del dardo. Sólo que aquí empiezan los problemas. Si hay una posibilidad mayor que cero de que se alcance este punto, entonces hay una probabilidad mayor que cero para todos los demás puntos, de que sean alcanzados por el dardo. Sin embargo, hay un número infinito de puntos en nuestro blanco.
Si se suman las probabilidades de todos los puntos, se llega a la conclusión de que todo el blanco tiene una probabilidad infinita de ser alcanzado, lo cual no tiene sentido, ya que esta probabilidad no puede ser superior al 100%.
¿Y qué pasa si nos imaginamos que la probabilidad de ser golpeado es cero? Si la probabilidad de acertar a ese punto particular es cero, entonces es cero para todos los otros puntos, y si sumamos las probabilidades de todos los puntos de dar en el blanco, esta es cero. Pero tenemos la certeza de que el punto será alcanzados, entonces, ¿cómo puede ser cero?
4. Duplicando tú dinero.
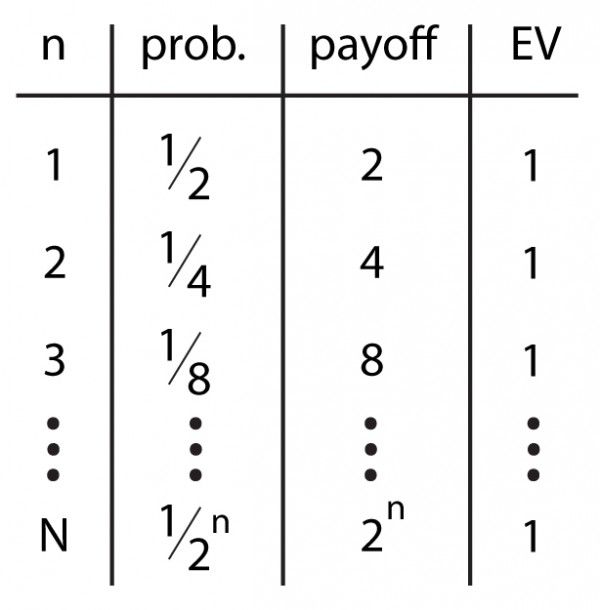
Imagine que un casino está promocionando un nuevo juego. El juego comienza con un peso en el banco de apuestas. Una persona lanza una moneda. Si sale sol, lo que está en el banco de apuestas se duplica, si sale águila, el juego termina y el jugador gana lo que tenga en el banco de apuestas.
¿Cuánto pagaría usted para entrar en este juego? ¿O cuánto sería justo cobrar para el casino? Si sabe un poco de matemáticas puede haber oído hablar de «esperanza matemática«, es decir, un juego que implica probabilidad de ganancia esperada. Y ¿cuál es la ganancia esperada en este juego?
La mayoría probablemente apostaría $5.00, tal vez un poco más, pero lo que la matemática dice es: «apuesta lo que tengas, la esperanza de ganancia es infinita«. El jugador tiene probabilidad del 50% de ganar $1.00, 25% de probabilidad de ganar $2.00, 12.5% de ganar $4.00 y así sucesivamente. El valor esperado es la suma de la probabilidad multiplicada por el valor del premio, así:
E = 1/2 + 1/2 + 1/2 + 1/2 + …
Esta es una suma infinita de fracciones de 1/2, y el resultado es infinito. Es decir, matemáticamente hablando, la esperanza matemática de ganancia es infinita. Pero, paradójicamente, muy pocas personas están dispuestas a pagar algo más de $20.00 por este juego (conocido como la paradoja de St. Petersburg).
Obviamente, estamos hablando de un casino hipotético, capaz de poner cuanto dinero sea necesario en el banco de apuestas. En la práctica, habría un límite para la máximo apuesta, y también para el número máximo de movimientos (nadie va a estar lanzando una moneda infinitamente). Quizás la paradoja surge de aquí: nadie espera o consigue entender un casino que pueda cubrir un premio infinito o una serie infinita de soles en una serie infinita de lanzamientos de moneda.
[Math is Fun, Ask Dr. Math, Good Math, Bad Math, Numberphile]
¿Puedo hacer dos preguntas?
Una es la ya hecha la otra requiere un poco de explicación, a ver si alguien puede o quiere responderla. La cuestión trata del cardinal de dos conjuntos (número de elementos que contienen). En matemáticas se dice que dos conjuntos tienen el mismo cardinal (es decir tienen el mismo número de elementos) si existe al menos una aplicación biyectiva de uno en otro, para mí esto es una extrapolación de los conjuntos finitos a los infinitos, ya que si por ejemplo tengo un conjunto formado por cuatro sillas y otro formado por 4 personas puedo asignar una silla a cada persona, de manera tal que todas las personas queden sentadas. Hasta aquí parece lógico todo, pero si nos paramos a pensar un poco más , lo que resulta en verdad es que puedo asignar cualquier silla a cualquier persona o cualquier persona a cualquier silla, es decir, cualquier aplicación inyectiva del primer conjunto sobre el segundo o viceversa, resulta ser también biyectiva, ya sé que ser biyectiva implica ser infectivo y no al contrario, pero cuando dos conjuntos finitos tienen el mismo número de elementos el ser inyectivo implica también el ser biyectivo . Siguiendo con el ejemplo: puedo asignar la silla 1 a la persona 1, la silla 2 a la persona 2, la tres a la tres y la cuatro a la cuatro, pero también puedo asignar la silla 1 a la persona 2 , la silla dos a la persona 1 , la silla 3 a la persona 4 y la silla 4 a la persona 3, etc. y cada una de ellas, además de ser aplicaciones invectivas , también serán biyectivas. Por tanto podríamos reformular la definición de cardinal como sigue: Dos conjuntos tienen el mismo cardinal si ocurre alguna de estas dos condiciones:
1. son el mismo conjunto
2. cualquier aplicación inyectiva del primer conjunto sobre el segundo o del segundo sobre el primero, es también biyectiva.
La idea es evitar la paradoja que surgió con los conjuntos infinitos en los que había subconjuntos con el mismo número de elementos que el conjunto que contiene a ese subconjunto, como ocurre con los naturales pares. Como se explica en el video. Y aquí va la pregunta. ¿Cuál es el inconveniente de aceptar la definición que se me ha ocurrido a mí y que resolvería la paradoja antigua antes mencionada? Pienso que no puedo ser el único al que se le haya ocurrido antes esa forma de plantear el infinito y sí no fue aceptado debe ser por alguna razón, por eso me gustaría saber cuál es.
Hay una paradoja, que no llego a entender bien pero sobretodo no sé como se llama. Es la paradoja de las infinitas bolitas numeradas que se van metiendo y sacando en una bolsa de la siguiente manera: en el primer día se meten las numeradas del 1 al 10 y se saca la número 1, el segundo día se meten las numeradas de la 11 a la 20 y se saca la numerada con el número 2, etc. La pregunta es ¿ cuántas bolas hay cuando pasen infinitos días?
Hotel de Hilbert.
Si está lleno, no pueden moverse los viajeros y cambiar de habitacion, por que esta lleno, si pueden moverse, es que hay habitaciones libres por lo tanto lo que me da a entender de la paradoja, es que las habitaciones son infinitas pero los viajeros no. En el caso de que los viajeros pudieran ser tambien infinitos, para que los viajeros tengan habitacion libre, el valor infinito de los hoteles tendra que ser superior o igual al valor infinito de los viajeros en ese momento. Si nos el viajero tendrá que esperar a que aumente el valor infinito de habitaciones.
por mi se pueden meter sus paradojas por el asterisco y asi sentir un placer infinito…
lo del hotel infinito…el problema no es que no haya habitacion que si la hay es un hotel infinito, el problema es lo que tiene que caminar el huesped para llegar a su habitacion que a de estar hasta la ching..da
Infinitos huéspedes = a infinitas habitaciones, son la misma cantidad nunca quedará una habitación vacía, si llega a suceder, buscamos uno de los huéspedes infinito que tenemos y lo metemos allí. jajaja. es un bucle.
Olvidaron los dos clásicos: la paradoja de Aquiles y la tortuga: si hay una carrera entre Aquiles y una tortuga dando ventaja a la tortuga, Aquiles nunca le ganará, porque para cuando llegue a donde estaba la ventaja de la tortuga, la tortuga ya avanzo un tramo, para cuando alcance dicho punto, la tortuga ya avanzo, etc. Como algunas de las indicadas en el post, el error en esta paradoja es asumir que una suma de infinitos términos necesariamente es infinita.
El otro es la demostración de Cantor de los números transfinitos, ie. Hay conjuntos con más miembros que lo que se conoce como infinito – que es sólo la cardinalidad (es el término correcto, acuérdense que el infinito no es un número)del conjunto de números naturales. Usando una técnica parecida a la de las habitaciones de Hilbert, demuestra que el conjunto de todos los puntos de un segmento de recta tiene más miembros que el conjunto de números naturales, o lo que es lo mismo, hay más números reales que números naturales (si piensan que es obvio porque los números reales incluyen fracciónes, raíces cuadradas y números como pi, resulta que el conjunto de todos los números racionales si tiene tantos miembros como el conjunto de números reales) Tuve mi momento eureka cuando logre entender esto, es muy recomendable.
Creo que varias de las paradojas estan mal redactadas y no quedan bien planteadas pero gracias buscaré las fuentes originales. Me parecieron muy interesantes…
Tsss ese Dan si me caso <3
el cuarto se hiso «trampa» ya que estan utilizando la formula de esperanza matematica con una variable discreta, cuando la variable propuesta es continua.
En la variable discreta se tiene la formula que se determina en el «problema»
Mientras que en la variable continua se tiene una integral
Aclare mejor su punto, porque si bien se trata de matemáticas discretas, no recuerdo que haya una prohibición de no hacer experimentos repetidos, o que no pueda haber infinitas repeticiones de experimentos discretos (aunque sí es el caso el casino debe prever tener una provisión infinita de martinis también) es increíble que así como se plantea nadie entre, porque no hay una condición en la cual pierdas el dinero. Creo que esta paradoja debe ser más compleja de lo que se escribió en el post.
la verdad esta ultima paradoja no me quedo muy clara, y tambien yo creo que le falta y debe de tener mas informacion, en lo que me base para decir esto fue que segun lo que investigue y recuerdo un poco la formula esta mal planteada ya que la formula para la esperanza matematica se puede tomar de dos formas
la primera es la de variable aleatoria discreta y para poder considerar nuestra variable como aleatoria discreta se debe de poder tomar un numero finito de valores dentro de un intervalo, pero nuestros valores son infinitos por lo que no entra en esta definicion
la segunda formula es necesario que la variable sea una variable aleatoria absolutamente continua es decir si existe una función real f, positiva e integrable en el conjunto de números reales, con ello si podemos tomar valores infinitos
lo unico que queria recalcar es que la formula para la esperanza matematica de una variable aleatoria absolutamente continua es diferente de la que manejan aqui, y es una integral
el primero es demaciado estupido ya que si la «solucion» a la habitacion es mover a un huesped eso implicaria que la infinidad de huespedes es menor a la infinidad de habitaciones lo cual no puede ser
el segundo es simplemente hacer «trampa» puesto que si el volumen se considera finito ya que como se esta estrechando este cada vez va incrementando menos por lo que se dice que tiende a un numero x pero la superficie va aumentando cada vez mas, es una asintota
el tercero esta mal planteado, ya que solo con que estemos pensando en un blanco dentro de un sistema de 3 coordenadas, este blanco tiene un área determinada y podra tener un enorme numero de puntos dentro de el que jamas terminariamos ni en millones de años en contarlos, pero no son infinitos por lo que la suma de las probabilidades no sería infinita, será muy pequeña pero no infinita
Sobre el primero justo en eso consiste la paradoja, sólo ilustra la propiedad de que uno más infinito sigue siendo infinito. La paradoja se resuelve indicando -como se dijo al principio- que el infinito no es un número, y por lo tanto las operaciones aritméticas no son legítimas en el.
El embudo de toricelli ese si me vuela la mente, pero en el cálculo infinitesimal hay esa clase de cosas (hace 13 años que no estudio nada del tema) vale la pena googlearlo.
El tema de los dardos si parece estar mal tratado. Es común en cálculo que una suma de infinitos términos infinitesimales de un valor finito. La trampa aquí consiste en que no existe la probabilidad de tocar un punto matemático, lo que en estadística se hace es calcular la probabilidad sobre un área, digamos un puntito de 10 millonésimas de radio, y sumando las áreas separadas en todo el círculo si da 100%. Si ahora calculamos sobre un puntito 100 veces menor, seguiremos sumando 100%, porque las probabilidades de cada punto son menores, pero hay más puntos. Si podemos repetir infinitamente el proceso, pero nunca llegaremos a un punto de radio cero, así que en el planteamiento de esta paradoja se confunde llegar al infinitesimal con el «paso al límite», que matemáticamente no es la misma cosa, confundirlos es un error común en los estudiantes de bachillerato
le estas diciendo a dan o al q tradujo esto morro de bachilleraro xD? por q tu y dan escribieron practicamente lo mismo
¿Sabes lo que dices con la primer paradoja???
la paradoja dice que (infinito + 1 = infinito)
tu dices que no tiene sentido que un infinito «huéspedes» sea menor que otro infinito «habitaciones», pero eso NO es lo que implicaría
Lo que implicaría es que infinito mas cualquier numero es igual a INFINITO.
infinito (huéspedes) + 1 (numero para moverse a siguiente habitación) es igual a que los infinitos huéspedes sigan siendo infinitos (ninguno mas grande que otro).
La paradoja de Hilbert es mas compleja de lo que planteas primero son dos millonarios que quieren hacer el hotel mas grande del mundo y se dan cuenta que solo haciendo un hotel infinito nadie los va a superar.
La primera paradoja es hay infinito cantidad de numeros
La segunda para meter infinitos huespedes necesitas saber que dentro de los numeros infinitos hay infinitos numeros pares e impares
La tercera hay infinitos numeros primos.
La paradoja de Hilbert podria continuar
BRAIN EXPLODE!
SOLO HAY DOS COSAS INFINITAS, EL UNIVERSO Y LA ESTUPIDEZ HUMANA, Y DE LA PRIMERA NO ESTOY TAN SEGURO.
ALBERT EINSTEIN
«Imagínese un hotel de infinitas habitaciones en el que todas están ocupadas.» No me lo imagino: si tiene infinitas habitaciones significa que siempre hay habitaciones disponibles por muy lleno que esté.
Es como decir «Imaginese un pato blanco que es negro», o es blanco o es negro.
Has de ser licenciado, si tienes infinitas habitaciones e igual cantidad de huéspedes (es decir infinitos) entonces esta lleno, como decir, si tienes 1 habitación y tienes 1 huésped, entonces esta lleno, de igual manera si tienes 2 habitaciones y 2 huéspedes entonces esta lleno, al igual que 3 habitaciones con 3 huéspedes quiere decir lleno,
4 habitaciones con 4 huéspedes = lleno
5 habitaciones con 5 huéspedes = lleno
6 habitaciones con 6 huéspedes = lleno
7 habitaciones con 7 huéspedes = lleno
8 habitaciones con 8 huéspedes = lleno
9 habitaciones con 9 huéspedes = lleno
10 habitaciones con 10 huéspedes = lleno
…
infinitas habitaciones con infinitos huéspedes = lleno, espero que hayas entendido y haber acabado con un posible político mas.
para los que se preguntan cómo meter infinitos huéspedes, diré que el huésped de la habitación 1 se pase a la habitación 2, el que estaba eb la 2 se pasa a la 4, etcétera
quedan infinitas habitaciones impares